Vega is also a commonly used ratio and is also considered a greek, although it is not actually a Greek letter (some purists prefer to use the Greek letter tau for vega). Since most of these ratios are represented by Greek letters - delta, gamma, theta, and rho - the group is often referred to simply as the greeks. Several ratios have been developed to measure this change in price with respect to the price or volatility of the underlying and the effect of time decay. For example, a Delta of 0.The Option Greeks: Delta, Gamma, Theta, Vega, and Rho › Money › Options The Option Greeks: Delta, Gamma, Theta, Vega, and Rhoīecause the price of options depends on the price of the underlying asset and because options are a wasting asset due to their limited lifetimes, option premiums vary with the price and volatility of the underlying asset and time to expiration of the options contract. You can think of Delta, as the probability that a given option will expire in the money. The Delta of out-of-the-money put options will get closer to 0.0 as expiration approaches.The Delta of in-the-money put options will get closer to -1.00 as expiration approaches.The Delta will decrease (and approach -1.00) as the option gets deeper in the money.At-the-money options usually have a Delta near -0.50.Have a negative Delta that can range from 0.0 to -1.00.
The Delta of out-of-the-money call options will get closer to 0.0 as expiration approaches. The Delta of in-the-money call options will get closer to 1.00 as expiration approaches. The Delta will increase (and approach 1.00) as the option gets deeper in the money. At-the-money options usually have a Delta near 0.50. Have a positive Delta that can range from 0.0 to 1.00. For example, a Delta of 0.40 means that the option’s price will theoretically move $0.40 for every $1 move in the price of the underlying stock or index. The first Greek is Delta, which measures how much an option's price is expected to change per $1 change in the price of the underlying security or index. Now, let's define each Greek in more detail. If we know that an option loses value over time, we can use Theta to approximate how much value it loses each day. For example, if we know that an option typically moves less than the underlying stock, we can use Delta to determine how much it is expected to move when the stock moves $1. Since there are a variety of market factors that can affect the price of an option in some way, assuming all other factors remain unchanged, we can use these pricing models to calculate the Greeks and determine the impact of each factor when its value changes. They are calculated using a theoretical options pricing model. Greeks, including Delta, Gamma, Theta, Vega and Rho, measure the different factors that affect the price of an option contract. Simulate the effect of interest rate changes on an option (Rho). Understand how sensitive an option might be to large price swings in the underlying stock (Vega). 
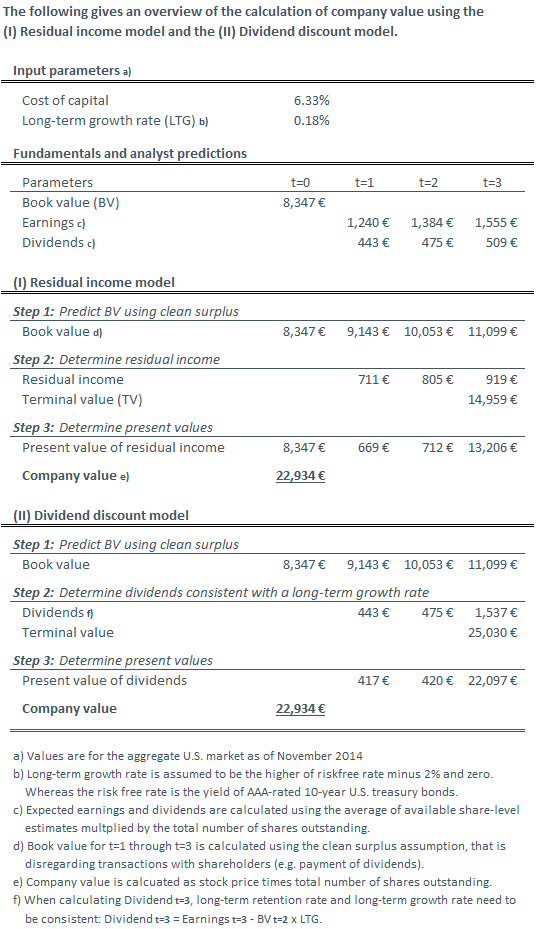
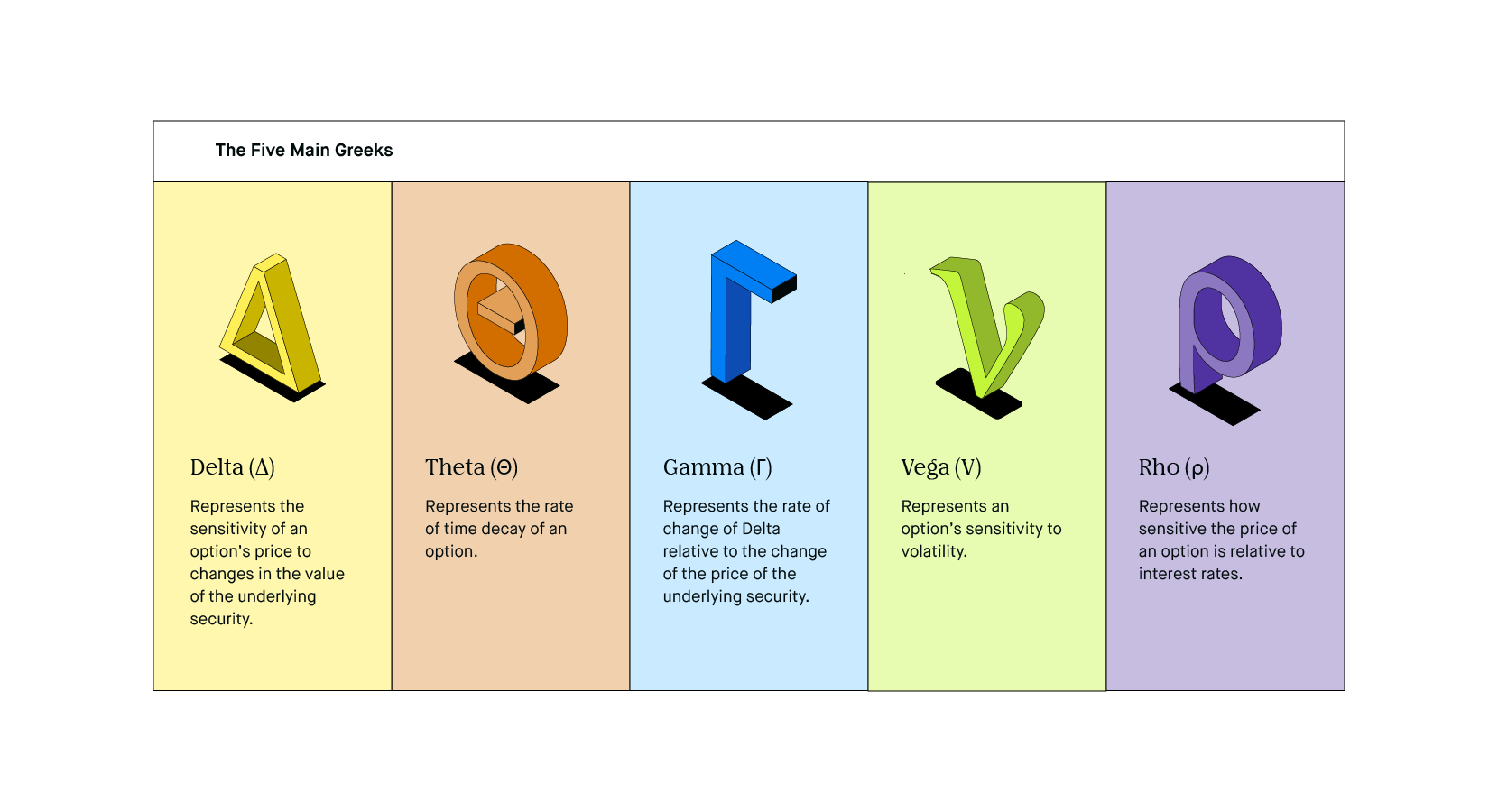Get a feel for how much value your option might lose each day as it approaches expiration (Theta). Estimate how much the Delta will change when the stock price changes (Gamma). Gauge the likelihood that an option you’re considering will expire in the money (Delta). Consider some of the things Greeks may help you do: What can option Greeks do for you?Īrmed with Greeks, an options trader can make more informed decisions about which options to trade and when to trade them. Read on, and we will explain what these Greek letters mean and how they can help you to better understand and evaluate the price of an option. If you're an options trader, you may have heard about “Greeks,” but perhaps you don’t know exactly what they are or, more importantly, what they can do for you. Meet the experts behind Schwab's investing. 
Understanding these principles can help.Schwab Live Webcasts and Special Events.Discover how easy it is to transfer assets to Schwab.Benefits and Considerations of Mutual Funds.
0 kommentar(er)
